Reference angles are used to determine the values of the trigonometric functions in the second, third and fourth quadrants, in particular, for the "nice" angles. The reference angle for an angle θ is the smallest angle φ from the (positive or negative) x-axis to the terminal ray of the angle θ.

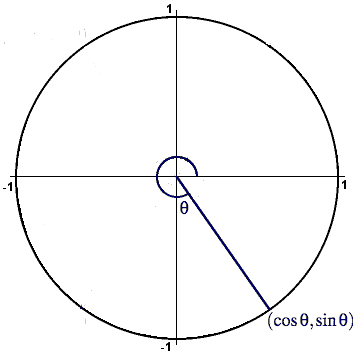
For an angle θ in the fourth quadrant the reference angle φ is the remaining angle needed to complete a full circle angle, that is, 2π radians or 360°. Thus θ + φ = 2π or θ + φ = 360°, and so

φ = 2π - θ or φ = 360° - θ.

Next plot the reference angle φ in the first quadrant, that is, in standard position. We see that the point (cos θ, sin θ) is the reflection of the point (cos φ, sin φ) in the x-axis. The x-coordinates of these two points are equal, while the y-coordinates have opposite signs. Thus, for θ in Quadrant IV:

cos θ = cos φ and sin θ = - sin φ.

Conclusion: to compute the value of cosine and sine of an angle θ in the fourth quadrant, find the value of the function at the reference angle φ and then attach the correct sign (+ for cosine and - for sine in Quadrant IV). The method also works for the other trigonometric functions. For example, tan θ = - tan φ in Quadrant IV.

Restore initial diagram