The values of all six trigonometric functions can be represented as the lengths of various sides of triangles associated with the unit circle definition of cosine and sine. Notice that OB, OC and OP all have length 1. Also, ∠ POA = ∠ QOB = ∠ ORC = θ, and ∠ OAP = ∠ OBQ = ∠ RCO (all three are right angles). We will use these facts.

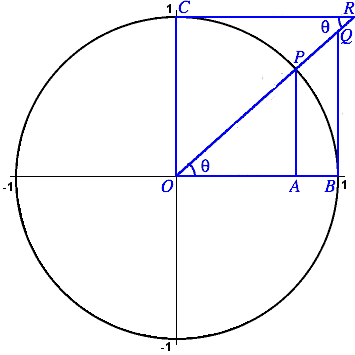
By definition the point P has coordinates (cos θ, sin θ). This means cos θ = OA and sin θ = AP.

The triangles OAP and OBQ are similar. The ratios of corresponding sides are therefore equal, for example, AP/OA = BQ/OB, that is, sin θ/cos θ = BQ/1. We have deduced that tan θ = BQ.

Using the same triangles, we see that OP/OA = OQ/OB, that is, 1/cos θ = OQ/1. This means that sec θ = OQ.

The triangles OBQ and RCO are similar. Therefore OB/BQ = CR/OC (note carefully which sides correspond), that is, 1/tan θ = CR/1. We conclude that cot θ = CR.

Finally, using the similar triangles OAP and RCO, we get OP/OA = OR/OC, that is, 1/sin θ = OR/1, and so csc θ = OR.

As a bonus, the theorem of Pythagoras applied to each the three right triangles in the diagram gives us the three fundamental trigonometric identities:

cos² θ + sin² θ = 1,

1 + tan² θ = sec² θ

and 1 + cot² θ = csc² θ.