Angles are measured in standard position from the positive horizontal axis going counter-clockwise (for the positive direction). One whole revolution is 360°. The circle is then divided up to find other nice angles.

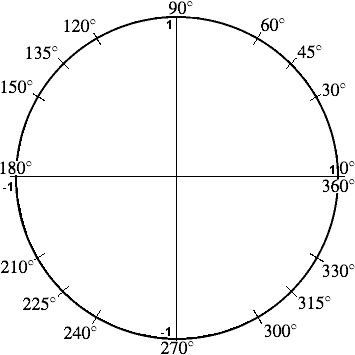
Half a revolution is therefore equal to 360°/2 = 180°. One quarter of a revolution (a right angle) equals 360°/4 = 90°. Three quarters of a revolution measures 3 × 90° = 270°.

One eighth of a revolution is the angle that divides the first quadrant in half; it is half a right angle: 360°/8 = 90°/2 = 45°. The angles that bisect the other quadrants are 90° + 45° = 135°, 180° + 45° = 225° and 270° + 45° = 315°.

The angle one third of the way through the first quadrant is one twelfth of a revolution, that is, 90°/3 = 360°/12 = 30°. Double 30° is two-thirds of the way through the first quadrant, or one sixth of a revolution: 2 × 30° = 360°/6 = 60°. The angles one third and two thirds of the way through the second, third and fourth quadrants are 90° + 30° = 120°, 90° + 60° = 150°, 180° + 30° = 210°, 180° + 60° = 240°, 270° + 30° = 300° and 270° + 60° = 330°.

Finally, let's not forget the angle with measure 0°.

In increasing order: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.

These are the "nice" angles. Of course, you can continue to subdivide one revolution to locate any angle you wish. Angles with measure greater than 360° complete one or more complete revolution(s) plus the remainder left when dividing the angle measure by 360. Angles with negative measure are taken in the clockwise direction.