The definition of the trigonometric functions cosine and sine in terms the coordinates of points lying on the unit circle immediately gives us the fact often known as the fundamental trigonometric identity.

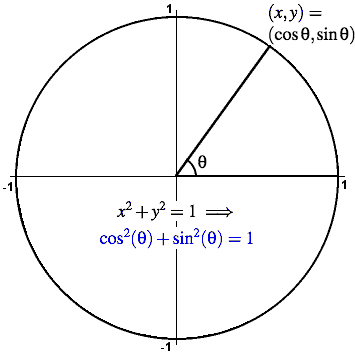
A point (x,y) on the unit circle satisfies the equation x² + y² = 1. For each angle &theta the point (cos θ, sin θ) is such a point (x,y) on the unit circle. We substitute this point (cos θ, sin θ) into the equation of the unit circle:

cos²(θ) + sin²(θ) = 1.

This equation is the fundamental trigonometric identity that turns out to be extremely useful in working with the trigonometric functions.

As a bonus we can quickly derive two other identities (sometimes also known as fundamental trigonometric identities).

First, divide each term of the fundamental identity by cos²(θ):

cos²(θ)/cos²(θ) + sin²(θ)/cos²(θ) = 1/cos²(θ),

that is,

1 + tan²(θ) = sec²(θ).

Second, divide each term of the fundamental identity instead by sin²(θ):

cos²(θ)/sin²(θ) + sin²(θ)/sin²(θ) = 1/sin²(θ),

that is,

cot²(θ) + 1 = csc²(θ).