The values of the trigonometric functions repeat, since once the angle θ exceeds one full revolution, the same points (x,y) on the unit circle are traced out as were traced out during the first revolution. A function f(x) that repeats like this is called a periodic function, and the smallest positive value k so that f(x+k) = f(x) for every x is called the period of f(x).

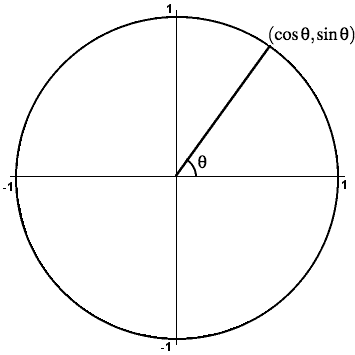
Starting from an angle θ, with associated point (cos θ, sin θ), advancing the angle one full revolution to θ + 2π = θ + 360° shows that (cos(θ + 2π), sin(θ + 2π)) = (cos(θ+360°), sin(θ+360°)) is the same point as (cos θ, sin θ). Therefore:

cos(θ + 2π) = cos θ & sin(θ + 2π) = sin θ,

or

cos(θ+360°) = cos θ & sin(θ+360°) = sin θ.

These identities are true for any angle θ, and there is no smaller angle φ so that either cos(θ + φ) = cos θ or sin(θ + φ) = sin θ holds for every angle θ. We conclude that sine and cosine have period 2π = 360°.

It's also true that tan(θ + 2π) = tan(θ+360°) = tan θ, but the period of tangent is not 2π. What is the period of tangent? Adding π = 180° to θ we see that the point (cos(θ + π),sin(θ + π)) = (cos(θ + 180°),sin(θ + 180°)) lies on the opposite side of the unit circle from the point (cos θ, sin θ). Therefore:

tan(θ + π) = sin(θ + π)/cos(θ + π) = (-sin θ)/(-cos θ) = sin θ/cos θ = tan θ

or

tan(θ+180°) = sin(θ + 180°)/cos(θ + 180°) = (-sin θ)/(-cos θ) = sin θ/cos θ = tan θ.

This identity is true for any angle θ, and there is no smaller angle φ so that tan(θ + φ) = tan θ holds for every angle θ. We conclude that tangent has period π = 180°.

Restore initial diagram