Why do we use two variables?

Students often question why two different variables x and t are used in the following form of the fundamental theorem of calculus:

Why not just use the variable x as the variable of integration as well as the upper limit? In short, because it over-uses the variable. Sure, using just one variable would make using the theorem easier (just write down the integrand without having to remember to replace the variable of integration by the upper limit variable), but it is confusing to do so. On this page we explain why two variables are used.

While it is technically correct to use the same variable for both the variable of integration and in one or both limits of integration, the roles played by the variables in the two locations differ. This is likely to be confusing. In a definite integral the variable of integration does not appear in the answer - in computer science terms, the variable of integration is a local variable. A variable appearing in a limit of integration, however, does appear in the answer. In the equation above, the result of the integral is a function of x (not t, the local variable). It's best to use a different variable for the variable of integration to avoid confusion. In most cases you will see different variables used.

The ideas of the previous paragraph are explored in more detail below.

A definite integral of the form

is really shorthand for

This definite integral represents the area under the function y=t² from t=0 to t=4. Likewise, if we write the integral

we mean the (signed) area under the function y=t² from t=0 to t=x, which gives an answer depending on the value of x. So this integral defines a function of x. In this integral we use the second variable t to describe the interval of integration 0 ≤ t ≤ x. If we used only the one variable x for both the variable of integration and the upper limit, we would be integrating over the nonsense interval 0 ≤ x ≤ x. So here we do need a second variable as the variable of integration.

To extend the explanation even further we examine part of one of the standard proofs of the fundamental theorem of calculus. The theorem provides the derivative of the function

where a is a constant (there are other technical conditions mentioned in the theorem). To find the derivative of this function A(x) we use the limit definition of the derivative:

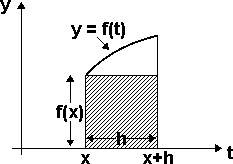
Without giving all the technical details, the proof concludes by observing that the integral of f(t) from t=x to t=x+h is approximately the area of the rectangle of height f(x) and width h (the hypothesis that y=f(t) is continuous is used at this point), and the approximation improves as h gets smaller. That area is thus approximately f(x)h, and, since h cancels in the numerator and denominator, the limit above is then computed to be f(x).

If the variable x were used as both the upper limit and as the variable of integration in the definition of A(x), then the integral in the proof would be over the nonsense interval x ≤ x ≤ x+h.

To summarize, listen to your teacher: two variables are commonly used. That means you need to be careful to use the correct variable in the answer to a derivative of an integral problem.

More:

• Variations
  • When the lower limit of the integral is the variable of differentiation
  • When one limit or the other is a function of the variable of differentiation
  • When both limits involve the variable of differentiation
  • Other tricks
• Common mistakes on derivative of integral problems
  • Common types of mistakes
  • The Common Calculus Mistakes section of mathmistakes.info includes mistakes on derivatives of integrals.