Using the fundamental theorem of calculus to find the derivative (with respect to x) of an integral like

seems to cause students great difficulty. We'll try to clear up the confusion.

Here's the fundamental theorem of calculus:

Theorem If f is a function that is continuous on an open interval I, if a is any point in the interval I, and if the function F is defined by

then the derivative of F(x) is F'(x) = f(x) for every x in the interval I.

(Sometimes this theorem is called the second fundamental theorem of calculus.)

Another way of stating the conclusion of the fundamental theorem of calculus is:

The conclusion of the fundamental theorem of calculus can be loosely expressed in words as: "the derivative of an integral of a function is that original function", or "differentiation undoes the result of integration".

This description in words is certainly true without any further interpretation for indefinite integrals: if F(x) is an antiderivative of f(x), then:

Example 1: Let f(x) = x³ + cos(x). The (indefinite) integral of f(x) is

The derivative of this integral is

so we see that the derivative of the (indefinite) integral of this function f(x) is f(x). (Reminder: this is one example, which is not enough to prove the general statement that the derivative of an indefinite integral is the original function - it just shows that the statement works for this one example.)

Now the fundamental theorem of calculus is about definite integrals, and for a definite integral we need to be careful to understand exactly what the theorem says and how it is used. Some of the confusion seems to come from the notation used in the statement of the theorem.

The first thing to notice about the fundamental theorem of calculus is that the variable of differentiation appears as the upper limit of integration in the integral:

Think about it for a moment. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative of that definite integral will be zero. Here are two examples of derivatives of such integrals.

Example 2: Let f(x) = e^x -2. Compute the derivative of the integral of f(x) from x=0 to x=3:

As expected, the definite integral with constant limits produces a number as an answer, and so the derivative of the integral is zero.

Example 3: Let f(x) = 3x². Compute the derivative of the integral of f(x) from x=0 to x=t:

Even though the upper limit is the variable t, as far as the differentiation with respect to x is concerned, t behaves as a constant. So the derivative is again zero.

The result is completely different if we switch t and x in the integral (but still differentiate the result of the integral with respect to x).

Example 4: Let f(t) = 3t². Compute the derivative of the integral of f(t) from t=0 to t=x:

This example is in the form of the conclusion of the fundamental theorem of calculus. We work it both ways. First, actually compute the definite integral and take its derivative. Second, notice that the answer is exactly what the theorem says it should be!

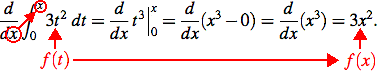
Note the important fact about function notation: f(x) is the same exact formula as f(t), except that x has replaced t everywhere.

The great beauty of the conclusion of the fundamental theorem of calculus is that it is true even if we can't (easily, or at all) compute the integral in terms of functions we know! The theorem says that provided the problem matches the correct form exactly, we can just write down the answer. In Example 4 we went to the trouble (which was not difficult in this case) of computing the integral and then the derivative, but we didn't need to. The theorem already told us to expect f(x) = 3x² as the answer. It also tells us the answer to the problem at the top of the page, without even trying to compute the nasty integral.

Example 5: Compute the derivative (with respect to x) of the integral:

By the fundamental theorem of calculus:

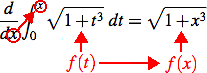
To make sure you understand the derivative of a definite integral, figure out the answer to the following problem before you roll over the expression to see the answer:

Example 6:

Notes: (a) the answer is valid for any x > 0; the function sin(t)/t is not differentiable (or even continuous) at t = 0, since it is not even defined at t = 0; (b) this problem cannot be solved by first finding an antiderivative involving familiar functions, since there isn't such an antiderivative. If an antiderivative is needed in such a case, it can be defined by an integral. (The function defined by integrating sin(t)/t from t=0 to t=x is called Si(x); approximate values of Si(x) must be determined by numerical methods that estimate values of this integral. By the fundamental theorem of calculus, the derivative of Si(x) is sin(x)/x.)

More:

• Why do we use two different variables?
• Variations
  • When the lower limit of the integral is the variable of differentiation
  • When one limit or the other is a function of the variable of differentiation
  • When both limits involve the variable of differentiation
  • Other tricks
• Common mistakes on derivative of integral problems
  • Common types of mistakes
  • The Common Calculus Mistakes section of mathmistakes.info includes mistakes on derivatives of integrals.