When both limits involve the variable of differentiation

The statement of the fundamental theorem of calculus shows the upper limit of the integral as exactly the variable of differentiation. If both limits involve the variable of differentiation, the derivative can be found once the integral is rewritten as the sum of two integrals using the property that if a, b and c all lie in an interval on which the function f(t) is continuous, then

(In the case a < b < c, this equation simply says the signed area under y=f(t) from t=a to t=c is the sum of the signed areas under y=f(t) from t=a to t=b and from t=b to t=c.)

So all we need to do is break the integral into two pieces at some constant value (keeping in mind that we'd like all the limits of the integrals to lie in some interval on which the function f(t) is continuous), and then reverse the limits of integration on the integral with the function as the lower limit (which changes the sign of the integral). The fundamental theorem of calculus then can be applied to each of the two integrals.

Example 1: Find

Break the integral at any fixed point, say x=0 (note this integrand is continuous everywhere). It does not matter that 0 does not lie between x and 2x (except in the case x=0):

So

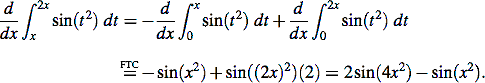
(The second derivative requires the use of the chain rule, since the upper limit is a function of x.)

See if you can provide the steps in the second example. Roll the mouse over each step once you've decided.

Example 2: Find

The restriction on x is made so that the integrand is continuous on an interval containing both limits - in this case we need -1 ≤ tan(x) ≤ 1, and the indicated interval for x meets that requirement for tan(x).

Break the integral into two pieces:

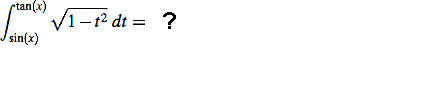
(Remove answer to the above step)

Compute the derivatives of the two integrals:

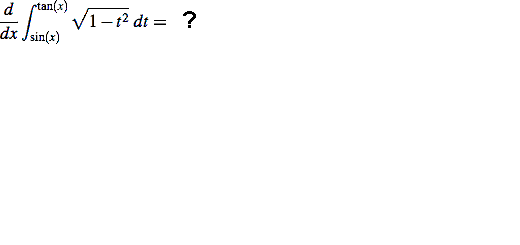
(Remove answer to the above step)

Notes: (1) the chain rule is used to find both derivatives;

(2) in the algebraic simplification to tidy up the answer we use the fact that cos(x) is positive for x in the interval -π/4 ≤ x ≤ π/4 to conclude that √(cos²(x)) = cos(x). We also recognize the double angle formula for cosine.

More:

• Why must we use two different variables?
• Other variations
  • When the lower limit of the integral is the variable of differentiation
  • When one limit or the other is a function of the variable of differentiation
  • Other tricks
• Common mistakes on derivative of integral problems
  • Common types of mistakes
  • The Common Calculus Mistakes section of mathmistakes.info includes mistakes on derivatives of integrals.