When a limit of integration is a function of the variable of differentiation

The statement of the fundamental theorem of calculus shows the upper limit of the integral as exactly the variable of differentiation. Using the chain rule in combination with the fundamental theorem of calculus we may find derivatives of integrals for which one or the other limit of integration is a function of the variable of differentiation.

Example 1: Find

To find this derivative, first write the function defined by the integral as a composition of two functions h(x) and g(x), as follows:

since

The derivative of a composition of two functions is found using the chain rule:

The derivative of h(x) uses the fundamental theorem of calculus, while the derivative of g(x) is easy:

Therefore:

Notice carefully the h'(g(x)) part of the answer: x² replaces x in tan(x³), giving tan((x²)³) = tan(x⁶).

We look at another example.

Example 2: Find

See if you can provide the answers to the steps leading to the answer. Roll the mouse over each of the following steps once you've decided. The first step is to identify the integral in this example as the composition h(g(x)):

(Remove answer to the above step)

Compute the derivatives of h(x) and g(x):

(Remove answer to the above step)

Therefore:

(Remove answer to the above step)

Once you see the pattern of use of the chain rule you don't have to write out all the intermediate steps. Notice the upper limit replaces the variable of integration wherever it appears in the integrand and the result is multiplied by the derivative of the upper limit:

(This formula literally is just the chain rule, since f is the derivative of its antiderivative (given by the indefinite integral) - in the notation of the earlier examples, h'(x) = f(x).)

Example 3:

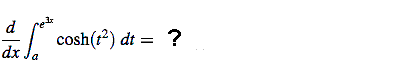
(Remove answer to the above step)

More:

• Why must we use two different variables?
• Other variations
  • When the lower limit of the integral is the variable of differentiation
  • When both limits involve the variable of differentiation
  • Other tricks
• Common mistakes on derivative of integral problems
  • Common types of mistakes
  • The Common Calculus Mistakes section of mathmistakes.info includes mistakes on derivatives of integrals.