By opposite angles we mean two angles that differ by a straight angle, that is, by π = 180°.

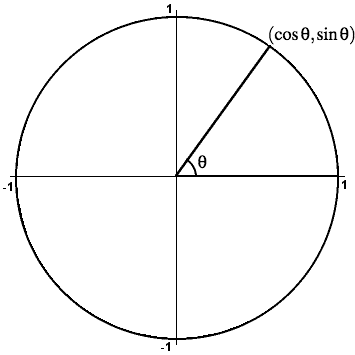
The angle opposite θ has measure θ + π = θ + 180°. Thus Q has coordinates
(cos(θ + π),sin(θ + π)) =
(cos(θ + 180°),sin(θ + 180°)).

The point on the opposite side of the unit circle from (a,b) is the point (-a,-b). So Q also has coordinates (-cos(θ),-sin(θ)). Therefore:

cos(θ+π) = -cos θ &
sin(θ+π) = -sin θ

or

cos(θ+180°) = -cos θ &
sin(θ+180°) = -sin θ.

These are the opposite angle identities.

Although the diagram shows the angle θ in the first quadrant, the same conclusion can be reached when θ lies in any quadrant, and so the opposite angle identities hold for all angles θ.

Restore initial diagram