The trigonometric functions sine and cosine are defined in terms of the coordinates of points lying on the unit circle x² + y²=1.

Start by constructing the ray from the origin at angle θ (measured counter-clockwise from the positive x-axis). This ray meets the unit circle at a point P = (x,y).

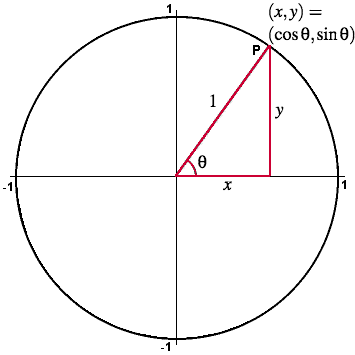
Cosine of the angle θ is defined to be the horizontal coordinate x of this point P:

cos(θ) = x.

Sine of the angle θ is defined to be the vertical coordinate y of this point P:

sin(θ) = y.

As θ changes so does the position of the point P and thus the values of cos(θ) = x and sin(θ) = y also change. In this way the functions f(&theta) = cos(θ) and g(&theta) = sin(θ) are defined.

Right away the unit circle gives us properties of the cosine and sine functions. Since the point P lies on the unit circle, both the cosine and sine functions have range -1 to 1. We also see that the points at the right, top, left and bottom of the circle give the values:

cos(0) = cos(0°) = 1 and sin(0) = sin(0°) = 0

cos(π/2) = cos(90°) = 0 and sin(π/2) = sin(90°) = 1

cos(π) = cos(180°) = -1 and sin(π) = sin(180°) = 0

cos(3π/2) = cos(270°) = 0 and sin(3π/2) = sin(270°) = -1

By using the geometric properties of the unit circle definition we can easily discover many other properties of the trigonometic functions. We look at many of these properties in the other parts of this unit circle activity.