Angles are measured in standard position from the positive horizontal axis going counter-clockwise (for the positive direction). One radian is defined to be the angle so that the arc of the unit circle subtended by that angle has length 1 (one radian is about 57.2958°). Since the circumference of the unit circle is 2πr = 2π (the radius of the unit circle is r = 1) and the angle is in direct proportion to the arc length, one whole revolution measures 2π radians. The circle is then divided up to find the radian measure of other nice angles.

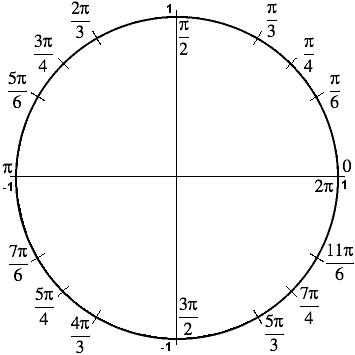
Half a revolution is therefore equal to 2π/2 = π radians. One quarter of a revolution (a right angle) equals 2π/4 = π/2 radians. Three quarters of a revolution measures 3 × π/2 = 3π/2 radians.

One eighth of a revolution is the angle that divides the first quadrant in half; it is half a right angle: (π/2)/2 = 2π/8 = π/4 radians. The angles that bisect the other quadrants are π/2 + π/4 = 3π/4 radians, π + π/4 = 5π/4 radians and 3π/2 + π/4 = 7π/4 radians.

The angle one third of the way through the first quadrant is one twelfth of a revolution, that is, (π/2)/3 = 2π/12 = π/6 radians. Double π/6 is two-thirds of the way through the first quadrant, or one sixth of a revolution: 2 × π/6 = 2π/6 = π/3 radians. The angles one third and two thirds of the way through the second, third and fourth quadrants are π/2 + π/6 = 3π/6 + π/6 = 2π/3 radians, π/2 + π/3 = 3π/6 + 2π/6 = 5π/6 radians, π + π/6 = 7π/6 radians, π + π/3 = 4π/3 radians, 3π/2 + π/6 = 9π/6 + π/6 = 5π/3 radians and 3π/2 + π/3 = 9π/6 + 2π/6 = 11π/6 radians.

Finally, let's not forget the angle with measure 0 radians.

The "nice" angles in increasing order: 0, π/6, π/4, π/3, π/2, 2π/3, 3π/4, 5π/6, π, 7π/6, 5π/4, 4π/3, 3π/2, 5π/3, 7π/4, 11π/6, 2π.

Of course, you can continue to subdivide one revolution to locate any angle you wish. Angles with measure greater than 2π complete one or more complete revolution(s) plus the remainder left when dividing the angle measure by 2π. Angles with negative measure are taken in the clockwise direction.