The Goal

Approximate (to two decimal place accuracy) the remaining parts of all possible triangles ABC with α = 54°, a = 6 and b=7 (where the side a is opposite the angle α, the side b is opposite the angle β and the side c is opposite the angle γ).

The Mistake

Find the mistake:

By the Law of Sines,

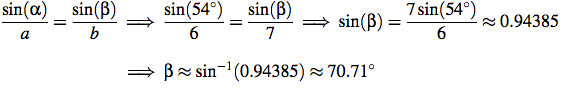
Since the angles in a triangle add to 180°, the third angle γ ≈ 180° - 54° - 70.71° = 55.29°. Apply the Law of Sines a second time to find c:

We conclude that the remaining parts of the triangle are β ≈ 70.71°, γ ≈ 55.29° and c ≈ 6.10.

(Roll the mouse over the math parts to see a hint in red)

The Correction

By the Law of Sines,

(Roll the mouse over the area above to see the correction in blue)

Therefore it is possible that there are two triangles, one of which may have an obtuse angle β. Consider each possibilty.

I. If β ≈ 70.71°, then (as above) the third angle γ ≈ 180° - 54° - 70.71° = 55.29°. Apply the Law of Sines to find c:

The remaining parts of the triangle in this case are β ≈ 70.71°, γ ≈ 55.29° and c ≈ 6.10.

II. If β ≈ 109.29°, then the third angle γ ≈ 180° - 54° - 109.29° = 16.71°. Since the angle γ turns out to be positive, there is a second triangle. Once again, apply the Law of Sines to find c in this case:

The remaining parts of the triangle in this case are β ≈ 109.29°, γ ≈ 16.71° and c ≈ 2.13.

An Explanation

The key in problems using the Law of Sines is to remember that there are two angles between 0° and 180° whose sines have the same value. If θ is an angle in the first quadrant, then the angle in the second quadrant with the same value for the sine function is 180° - θ.