The Goal

Solve the following equation for t:

The Mistake

Find the algebra mistake:

(Roll the mouse over the algebra to see a hint in red)

The Correction

(Roll the mouse over the area above to see the correction in blue)

An Explanation

It is no help in solving a quadratic equation to arrange it in the form at² + bt = c (unless c = 0) (in this problem, t² - 6t = 3) and then write it in the form t(at + b) = c (in this problem, t(t - 6) = 3). If c is not 0, you cannot conclude that t = c or at + b = c (in this case t = 3 or t - 6 = 3). In this problem you can check that neither 3 nor 9 are solutions of the original equation.
The number 0 is the only number with the property that if a product is equal to that number, then one of the factors is that number. If we had the equation t(t - 6) = 0 it would be true that t = 0 or t - 6 = 0.
There are three basic ways to solve a quadratic equation:
(1) factor (the equation t² - 6t - 3 = 0 does not easily factor, so use a different method)
(2) complete the square:

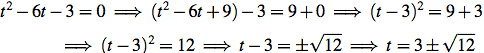
(3) use the quadratic formula: the solutions of at² + bt + c = 0 are

(see The Correction for the solution to the equation t² - 6t - 3 = 0 using the quadratic formula)