Example: Solving a trigonometric equation
Some problems provide the opportunity for more than one mistake.
The Goal
Solve the following equation for 0 ≤ x ≤ 2π:
The Mistakes
Find the mistakes:
1.
(Roll the mouse over the math to see a hint in red)
2.
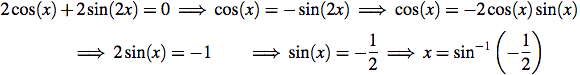
(Roll the mouse over the math to see a hint in red)
The Correction

(Roll the mouse over the area above to see the correction in blue)
Explanations
In the first mistake no use was made of the double angle formula for sine. The student then incorrectly produced tan(2x) from an expression that did not involve cos(2x) and, even if cos(2x) had appeared where cos(x) appears, would have been the reciprocal, namely cot(2x).
Two mistakes appear in the second attempted solution.
First of all, cos(x) is cancelled from the equation without considering that cos(x) = 0 might produce solutions (it does). A safer way to solve an equation with such a common factor is to rearrange with all nonzero terms on one side and then factor out the common factor. This makes it less likely that solutions arising from the common factor get overlooked.
The second mistake is that only one solution is produced, and even it does not lie in the domain requested. Care must be taken to use inverse trigonometric function values properly, taking into account the domain requested. In this example sine takes the value -1/2 at the angles 7π/6 and 11π/6 in the domain requested, while the inverse sine of -1/2 is -π/6, which is coterminal with 11π/6, but does not lie between 0 and 2π.