The Goal

Solve the following equation for c:

The Mistake

Find the algebra mistake:

(Roll the mouse over the algebra to see a hint in red)

The Correction

(Roll the mouse over the area above to see the correction in blue)

An Explanation

(In this explanation we cannot use c for the constant coefficient of a general quadratic since the variable in the quadratic is c. We use d instead.)
It is no help in solving a quadratic equation to arrange it in the form ac² + bc = d (unless d = 0) (in this problem, c² + 7c = 6) and then write it in the form c(ac + b) = d (in this problem, c(c + 7) = 6). If d is not 0, you cannot conclude that c = d (or ac + b = d) (in this case c = 6 (or c + 7 = 6)). You can check that neither 6 nor -1 are solutions of c² + 7c = 6.
The number 0 is the only number with the property that if a product is equal to that number, then one of the factors is that number. If we had the equation c(c + 7) = 0 it would be true that c = 0 or c + 7 = 0.
There are three basic ways to solve a quadratic equation:
(1) factor (the equation c² + 7c - 6 = 0 does not easily factor, so use a different method)
(2) complete the square:

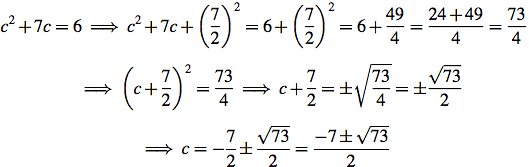
(3) use the quadratic formula: the solutions of ac² + bc + d = 0 are

(see The Correction for the solution to the equation c² + 7c - 6 = 0 using the quadratic formula)