Adding and subtracting fractions is not so hard once you understand why the rules for fractions work the way they do. For example, why do we need to find a "common denominator"? Let's use some examples to explain the idea.

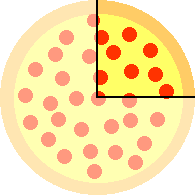
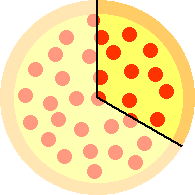
Example 1: You order two identical pizzas for a group of friends. One of the pizzas is cut into four slices and the other is cut into three slices. After everyone has eaten, there is one slice of each pizza left. How much of a whole pizza is left altogether? How should you cut the two remaining slices up into smaller slices so that all the new slices are the same size?

  +     =  

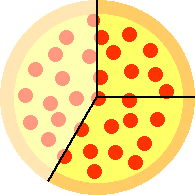
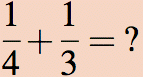
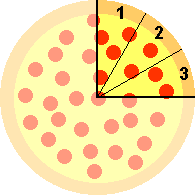
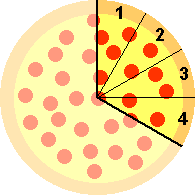
To figure out how much of a whole pizza is left we need to figure out how to divide each of the two remaining pieces into smaller equal sized pieces. This is where the common denominator comes in. The (smallest) common denominator is 12 (= 3 × 4, in this case). So we divide each of the two pieces into pieces of size equal to 1/12 of a whole pizza. Since 3/12 = 1/4 (cancel 3s), the first piece subdivides into 3 such pieces. The second piece subdivides into 4 of these smaller pieces, since 4/12 = 1/3 (cancel 4s). Then we can see how much of a whole pizza is left.

  +     =  

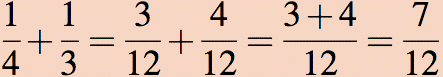
The two pieces together make 7/12 of a whole pizza, and we also see that we have cut the two pieces so that there are 7 smaller pieces of equal size. Notice that the numerator (7) tells us how many new pieces we have, each of size 1/12 of a whole pizza.

Finding a common denominator makes it possible to add two fractions because it allows us to write each fraction as a multiple of a common (usually smaller) fraction.

Subtracting fractions works the same way; find a common denominator so that the fractions involved are in the same terms.

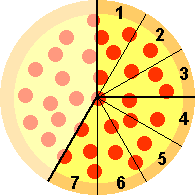
Example 2: You pull a pizza box out of the refrigerator and discover that it has three quarters of a pizza in it. You want to eat one third of the whole pizza. How should you cut the pizza into equal size slices so that you can take what you want? How many of these slices should you take and how much of the pizza will be left after you take your slices?

Click on the colored text when you think you have an answer for each step of the solution.

Write the fraction calculation for this problem. Click to see the answer. Click to remove answer.

  −     =  

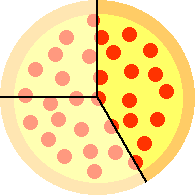
Find the common denominator. Click to see the answer. Click to remove answer.

Write the two fractions using the common denominator. Click to see the answer. Click to remove answer.

Subdivide the pizza pieces according to the fractions expressed with the common denominator. Click to show first piece slices. Click to make first piece whole. Click to show second piece slices. Click to make second piece whole. Click to show answer piece slices. Click to make answer piece whole.

Compute the answer to the fraction subtraction using the fractions in common denominator form. Click to see the answer. Click to remove answer.

The fraction calculation has been completed, but we still need to answer the questions asked at the start: How do we cut the two original pieces so that each new slice is an equal fraction of a whole pizza? How many of the smaller slices do you take to get a third of a whole pizza? How much of a whole pizza is left?
Click to see the answers. Click to remove answers.

Now that you see why a common denominator is needed (to put the fractions in the same terms), try the following examples without using pizza slices.

Example 3: Calculate

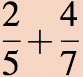
First step: find a common denominator. Click to see the answer. Click to remove answer.

Second step: write each fraction using the common denominator. Click to see the answer. Click to remove answer.

Third step: compute the sum using the fractions in common denominator form. Click to see the answer. Click to remove answer.

There is sometimes a fourth step: reduce the answer to simplest form, which means cancelling all common factors from the numerator and denominator.

Example 4: Calculate

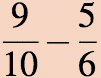
First step: find a common denominator. Click to see the answer. Click to remove answer.

Notice the common denominator need not be as large as the product of the denominators of the two fractions; the smallest common denominator is the least common multiple of the denominators.

Second step: write each fraction using the common denominator. Click to see the answer. Click to remove answer.

Third step: compute the sum using the fractions in common denominator form. Click to see the answer. Click to remove answer.

Fourth step: reduce the answer, that is, cancel common factors of the numerator and denominator. Click to see the answer. Click to remove answer.

Every addition and subtraction of fractions problem is computed using the steps in the examples on this page.